The problem is taken from kaggle.com. Based on historical data on bicycle rental and weather conditions, it is necessary to evaluate the demand for bicycle rental.
In the original problem statement, there are 11 features available. The feature set contains both real, categorical, and binary data. For the demonstration, a training sample bike_sharing_demand.csv is used from the original data.
See the Bike Sharing Demand, part 2 of the task where we performed advanced problem analysis.
import warnings
warnings.filterwarnings("ignore")
from sklearn import model_selection, linear_model, metrics import numpy as np import pandas as pd
%pylab inline
raw_data = pd.read_csv("bike_sharing_demand.csv", header = 0, sep = ",")
raw_data.head()
| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 81 | 0.0 | 3 | 13 | 16 |
| 1 | 2011-01-01 01:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 8 | 32 | 40 |
| 2 | 2011-01-01 02:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 5 | 27 | 32 |
| 3 | 2011-01-01 03:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0 | 3 | 10 | 13 |
| 4 | 2011-01-01 04:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0 | 0 | 1 | 1 |
datetime – hourly date + timestamp
season – 1 = spring, 2 = summer, 3 = fall, 4 = winter
holiday – whether the day is considered a holiday
workingday – whether the day is neither a weekend nor holiday
weather – 1: Clear, Few clouds, Partly cloudy, Partly cloudy 2: Mist + Cloudy, Mist + Broken clouds, Mist + Few clouds, Mist 3: Light Snow, Light Rain + Thunderstorm + Scattered clouds, Light Rain + Scattered clouds 4: Heavy Rain + Ice Pallets + Thunderstorm + Mist, Snow + Fog
temp – temperature in Celsius
atemp – “feels like” temperature in Celsius
humidity – relative humidity
windspeed – wind speed
casual – number of non-registered user rentals initiated
registered – number of registered user rentals initiated
count – number of total bike rentals, the target label
print(raw_data.shape)
(10886, 12)
Let us check is any values that are missing in dataset. If so, we need to process to fill them in.
raw_data.isnull().values.any()
False
The negative result shows there are no missed data cells/ values.
Features’ types
raw_data.info()
<class "pandas.core.frame.DataFrame"> RangeIndex: 10886 entries, 0 to 10885 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 datetime 10886 non-null object 1 season 10886 non-null int64 2 holiday 10886 non-null int64 3 workingday 10886 non-null int64 4 weather 10886 non-null int64 5 temp 10886 non-null float64 6 atemp 10886 non-null float64 7 humidity 10886 non-null int64 8 windspeed 10886 non-null float64 9 casual 10886 non-null int64 10 registered 10886 non-null int64 11 count 10886 non-null int64 dtypes: float64(3), int64(8), object(1) memory usage: 1020.7+ KB
We may see here that almost all the data are presented as numbers, whether integers or floating point ones.
Transform into the datetime type
So, let’s transform datetime feature (of a type object) into the datetime type in the dataframe:
raw_data.datetime = raw_data.datetime.apply(pd.to_datetime) raw_data.sample(3)
| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | month | hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4320 | 2011-10-12 01:00:00 | 4 | 0 | 1 | 3 | 22.96 | 26.515 | 83 | 8.9981 | 2 | 8 | 10 | 10 | 1 |
| 7355 | 2012-05-05 20:00:00 | 2 | 0 | 0 | 1 | 24.60 | 28.790 | 78 | 16.9979 | 100 | 209 | 309 | 5 | 20 |
| 9854 | 2012-10-14 23:00:00 | 4 | 0 | 0 | 2 | 22.96 | 26.515 | 68 | 19.0012 | 27 | 78 | 105 | 10 | 23 |
2 new features from datetime
Based on that transformed feature we calculate 2 new features: month and hour of the event (rental).
raw_data["month"] = raw_data.datetime.apply(lambda x : x.month) raw_data["hour"] = raw_data.datetime.apply(lambda x : x.hour)
raw_data.sample(3)
| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | month | hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6864 | 2012-04-04 08:00:00 | 2 | 0 | 1 | 2 | 18.04 | 21.970 | 72 | 7.0015 | 31 | 653 | 684 | 4 | 8 |
| 6290 | 2012-02-18 08:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 87 | 0.0000 | 10 | 92 | 102 | 2 | 8 |
| 3765 | 2011-09-07 20:00:00 | 3 | 0 | 1 | 3 | 26.24 | 28.790 | 89 | 6.0032 | 3 | 93 | 96 | 9 | 20 |
Splitting the model into the train and test sets.
Note that the data are time dependent, time spread. So we might get the train data of earlier period and evaluate the built estimator on the test set of later period. Since the data are sorted by time, we just cut of the last 1000 rows and use them as a test set.
train_data = raw_data.iloc[:-1000, :] hold_out_test_data = raw_data.iloc[-1000:, :]
print(raw_data.shape, train_data.shape, hold_out_test_data.shape)
(10886, 14) (9886, 14) (1000, 14)
print("train period from {} to {}".format(train_data.datetime.min(), train_data.datetime.max()))
print("evaluation period from {} to {}".format(hold_out_test_data.datetime.min(), hold_out_test_data.datetime.max()))
train period from 2011-01-01 00:00:00 to 2012-10-16 06:00:00 evaluation period from 2012-10-16 07:00:00 to 2012-12-19 23:00:00
Data and target function
We cut off the target, column count from the rest of dataset.
We also cut off the datetime data column since it’s now only an object identifier.
# training dataset train_labels = train_data["count"].values train_data = train_data.drop(["datetime", "count"], axis = 1)
# test dataset test_labels = hold_out_test_data["count"].values test_data = hold_out_test_data.drop(["datetime", "count"], axis = 1)
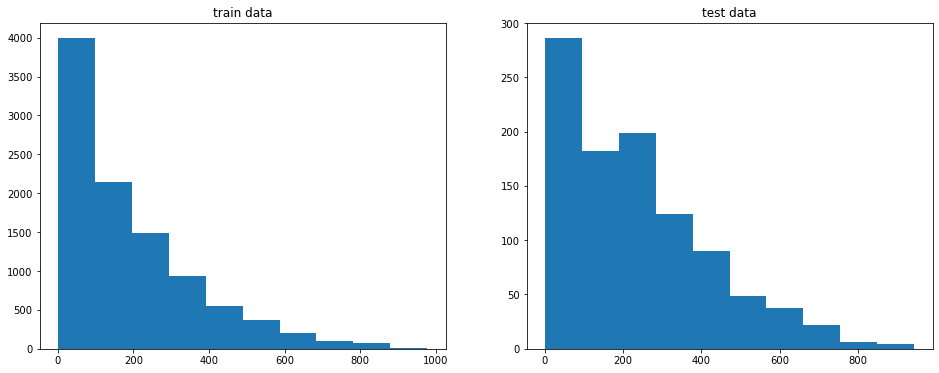
Let’s visualize the target function (label) at the train and test sets.
Remember that target label (count) shows how many bikes were rented at that time spot (hour).
pylab.figure(figsize = (16, 6))
pylab.subplot(1,2,1)
pylab.hist(train_labels)
pylab.title("train data")
pylab.subplot(1,2,2)
pylab.hist(test_labels)
pylab.title("test data")
Text(0.5, 1.0, "test data")
numeric_columns = ["temp", "atemp", "humidity",\ "windspeed", "casual", "registered", "month", "hour"]
train_data = train_data[numeric_columns] test_data = test_data[numeric_columns]
train_data.head()
| temp | atemp | humidity | windspeed | casual | registered | month | hour | |
|---|---|---|---|---|---|---|---|---|
| 0 | 9.84 | 14.395 | 81 | 0.0 | 3 | 13 | 1 | 0 |
| 1 | 9.02 | 13.635 | 80 | 0.0 | 8 | 32 | 1 | 1 |
| 2 | 9.02 | 13.635 | 80 | 0.0 | 5 | 27 | 1 | 2 |
| 3 | 9.84 | 14.395 | 75 | 0.0 | 3 | 10 | 1 | 3 |
| 4 | 9.84 | 14.395 | 75 | 0.0 | 0 | 1 | 1 | 4 |
We now train a model with SGDRegressor
SGDRegressor develops a model based on Stochastic Gradient Descent.
We supply the default paramets for the regressor model.
regressor = linear_model.SGDRegressor(random_state = 0, max_iter=5) regressor.get_params()
{"alpha": 0.0001,
"average": False,
"early_stopping": False,
"epsilon": 0.1,
"eta0": 0.01,
"fit_intercept": True,
"l1_ratio": 0.15,
"learning_rate": "invscaling",
"loss": "squared_loss",
"max_iter": 5,
"n_iter_no_change": 5,
"penalty": "l2",
"power_t": 0.25,
"random_state": 0,
"shuffle": True,
"tol": 0.001,
"validation_fraction": 0.1,
"verbose": 0,
"warm_start": False}
- Train the model
regressor.fit() - Estimate the model with MAE
mean_absolute_error
regressor.fit(train_data, train_labels) metrics.mean_absolute_error(test_labels, regressor.predict(test_data))
9340385490952.236
The number is too big…
Let’s output the targets and model predictions:
print("Target\n", test_labels[:10])
Target [525 835 355 222 228 325 328 308 346 446]
print("Prediction\n", regressor.predict(test_data)[:10])
Prediction [1.47320172e+13 2.64787988e+13 1.23495857e+13 1.35429951e+13 1.25998915e+13 1.74809610e+13 1.75786549e+13 2.11426913e+13 1.96417926e+13 2.32672606e+13]
The model predicts super big numbers. It should not be this way.
Let’s take a look at the regression coefficients.
regressor.coef_
array([ 1.12866511e+10, 6.68434729e+10, -7.05920006e+10, -2.09051100e+10,
1.65497847e+11, 2.92967602e+10, -6.71456293e+10, 8.32559786e+10])
The regression model coefficients are too high. This might happen if the features differ in scale.
Scaling the features
from sklearn.preprocessing import StandardScaler
We separately apply StandardScaler to the train and test data.
# create StandardScaler and train/fit it scaler = StandardScaler() scaler.fit(train_data, train_labels) scaled_train_data = scaler.transform(train_data) scaled_test_data = scaler.transform(test_data)
After we’ve got scaled data we train the model again.
regressor.fit(scaled_train_data, train_labels) metrics.mean_absolute_error(test_labels, regressor.predict(scaled_test_data))
0.11793762963431514
The error is in this case is very low.
If we output targets and predictions (below), we see that the model has done a good estimation. The distance is less than 1 bike.
print(test_labels[:10])
[525 835 355 222 228 325 328 308 346 446]
list(map(lambda x : round(x, 2), regressor.predict(scaled_test_data)[:10]))
[524.83, 834.83, 354.86, 221.89, 227.84, 324.88, 327.9, 307.93, 345.9, 445.9]
The regression result is suspiciously good
We take a look at the coefficients and see that almost all of the weights are too small.
#print(regressor.coef_)
map_obj = map(lambda x : round(x, 2), regressor.coef_)
print("regressor.coef_\n", list(map_obj))
regressor.coef_ [1.41, -1.41, 0.01, -0.04, 50.86, 148.0, -0.01, 0.01]
What are the features with non-small weights, 50.86, 148.0 ?
Casual and register features are.
How does the bike rental system work?
The bike rental system works as follows: both registered and unregistered users can use the system. In this case, column registered represent the number of registered users who use the system. The casual column shows the number of users who have not registered but also want to rent a bike.
Let’s output the values of the target function and see the following pattern: if the value of these two columns (registered and casual) is added together, we get our target label.
train_labels[:10]
array([16, 40, 32, 13, 1, 1, 2, 3, 8, 14], dtype=int64)
np.all(train_data.registered + train_data.casual == train_labels)
True
This was our mistake. We indeed used the features in dataset (casual, registered) that replicate the target, count.
So we cut off these data (columns) from train and test sets to properly build regession model.
train_data.drop(["casual", "registered"], axis = 1, inplace = True) test_data.drop(["casual", "registered"], axis = 1, inplace = True)
We scale the features with the new dataset and train/fit the model and estimate by MAE.
scaler.fit(train_data, train_labels) scaled_train_data = scaler.transform(train_data) scaled_test_data = scaler.transform(test_data)
regressor.fit(scaled_train_data, train_labels) metrics.mean_absolute_error(test_labels, regressor.predict(scaled_test_data))
121.81123864993025
The above MAE is more realistic.
The all model weights are influence the model predictions.
print(list(map(lambda x : round(x, 2), regressor.coef_)))
[31.03, 29.96, -41.93, 6.17, 14.08, 49.6]
Pipeline
Up to now we were solving the problem with default parameters of the regressor model. Now we have a certain base-level model.
Now we will select optimal parameters for a regressor model.
Yet to train/fit the model we need to scale [only] a train dataset. Since we use cross-validation (CV) we’ll need to scale each CV training dataset at each CV step. Therefore we make a Pipeline. Pipeline implies transformation chains. Particulary it’ll include 2 chains: (1) scaling and (2) regressotion itself at each iteration. Sklearn library does allow us to do both scaling of at each iteration and CV thru Pipeline module.
from sklearn.pipeline import Pipeline
# make a pipeline from two steps: scaling and classification
pipeline = Pipeline(steps = [("scaling", scaler), ("regression", regressor)])
# both methods `scaler` and `regressor` should posess methods fit() and perdict()
pipeline.fit(train_data, train_labels) metrics.mean_absolute_error(test_labels, pipeline.predict(test_data))
121.81123864993025
The error (above) remained the same. Pipeline works well.
Parameters selection
We select parameters by grid.
In the case of using Pipeline, we need to refer to the model parameters using the extended name.
First, we need to specify the name of the step, then a double underscore goes, then the name of the parameter itself follows.
pipeline.get_params().keys()
dict_keys(["memory", "steps", "verbose", "scaling", "regression", "scaling__copy", "scaling__with_mean", "scaling__with_std", "regression__alpha", "regression__average", "regression__early_stopping", "regression__epsilon", "regression__eta0", "regression__fit_intercept", "regression__l1_ratio", "regression__learning_rate", "regression__loss", "regression__max_iter", "regression__n_iter_no_change", "regression__penalty", "regression__power_t", "regression__random_state", "regression__shuffle", "regression__tol", "regression__validation_fraction", "regression__verbose", "regression__warm_start"])
We compose a dictionary of parameters to choose from.
parameters_grid = {
"regression__loss" : ["huber", "epsilon_insensitive", "squared_loss", ],
"regression__max_iter" : [3, 5, 10, 50],
"regression__penalty" : ["l1", "l2", "none"],
"regression__alpha" : [0.0001, 0.01],
"scaling__with_mean" : [0., 0.5], #
}
We build a CV grid and pass the pipeline object into it along with parameters_grid and others.
- Parameter scoring defines the kind of error that we score parameters at.
grid_cv = model_selection.GridSearchCV(pipeline, parameters_grid, scoring = "neg_mean_absolute_error", cv = 4)
%%time grid_cv.fit(train_data, train_labels)
Wall time: 22.6 s
GridSearchCV(cv=4,
estimator=Pipeline(steps=[("scaling", StandardScaler()),
("regression",
SGDRegressor(max_iter=5, random_state=0))]),
param_grid={"regression__alpha": [0.0001, 0.01],
"regression__loss": ["huber",
"epsilon_insensitive", "squared_loss"],
"regression__max_iter": [3, 5, 10, 50],
"regression__penalty": ["l1", "l2", "none"],
"scaling__with_mean": [0.0, 0.5]},
scoring="neg_mean_absolute_error")
print(grid_cv.best_score_) print(grid_cv.best_params_)
-108.61772632999148
{"regression__alpha": 0.01, "regression__loss": "squared_loss", "regression__max_iter": 3, "regression__penalty": "l2", "scaling__with_mean": 0.0}
Results of the CV grid parameters search
The CV parameters grid shows good result – neg_mean_absolute_error: -108.62
We are ok with 3 iterations – regression__max_iter: 3
Regularization parameter – regression__alpha: 0.01
Regularization type is L2, Ridge – regression__penalty: ‘l2’
As to the scaling, the best is with mean at the point 0 – scaling__with_mean: 0.0
metrics.mean_absolute_error(test_labels, grid_cv.best_estimator_.predict(test_data))
119.98978845935379
This error is less than one of the base model.
Yet, the MAE is at a certain point. What is the mean value of the test labels/targets?
np.mean(test_labels)
232.159
So, even though we’ve decreased the error from 122 to 120, since the mean is 232, the model has not underwent a good improvment.
test_predictions = grid_cv.best_estimator_.predict(test_data)
print(test_labels[:10])
[525 835 355 222 228 325 328 308 346 446]
print(test_predictions[:10])
[139.60470681 159.80765341 207.55935972 237.76288054 257.83836668 267.44558034 272.49537469 297.70688522 304.29818873 313.58821156]
The target and predictions of grid_cv differ siginificantly.
Targets-predictions graph
We display a graph of our objects in the space of the correct values of the target label vs our predictions. When we plot a graph in such a space a good model should have the following: a cloud of points in the diagonal area. It turns out that our predictions should coincide with the target label therefore the diagonal points should transpire.
pylab.figure(figsize=(16, 6))
# No parameters model setting
pylab.subplot(1,2,1)
pylab.grid(True)
pylab.scatter(train_labels, pipeline.predict(train_data), alpha=0.5, color = "red")
pylab.scatter(test_labels, pipeline.predict(test_data), alpha=0.5, color = "blue")
pylab.title("No parameters model setting")
pylab.xlim(-100,1100)
pylab.ylim(-100,1100)
# Grid search model setting
pylab.subplot(1,2,2)
pylab.grid(True)
pylab.scatter(train_labels, grid_cv.best_estimator_.predict(train_data), alpha=0.5, color = "red")
pylab.scatter(test_labels, grid_cv.best_estimator_.predict(test_data), alpha=0.5, color = "blue")
pylab.title("Grid search model setting")
pylab.xlim(-100,1100)
pylab.ylim(-100,1100)
(-100.0, 1100.0)
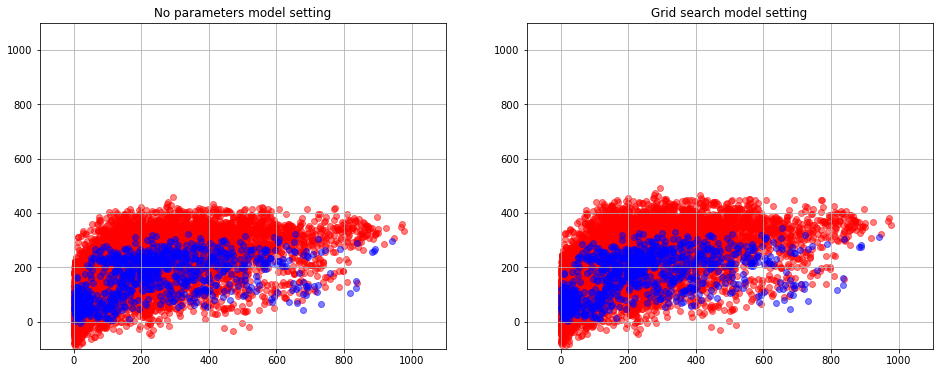
From the graph above we see that we have built a not very good model.
We see that our point clouds does not look like a diagonal. Moreover, point clouds when using a model without parameter selection and point clouds when using a model with parameter selection are not of much differece. That is, our model is quite weak, and optimization by parameters did not profit much.
Conclusion
In this post we touched a baseline, that is an initial regression model that works only on numerical features. We learned how to do scaling, how to build transformation chains.
In the followin posts we will try to improve this model by adding all the other features to it.
