In this post we’ll show how to make a linear regression model for a data set and perform a stochastic gradient descent in order to optimize the model parameters. As in a previous post we’ll calculate MSE (Mean squared error) and minimize it.
Contents
- Theory 1. Linear regression model and Gradient Decent (GD)
- Business case and input data
- Calculation of GD
- Theory 2. Stochastic Gradient Decent (SGD)
- Calculation of SGD
Intro
Linear regression analysis is one of the best ways to solve a problem of prediction, forecasting, or error reduction. The linear regression can be used to fit a predictive model to an observed data set of values (that we have) of the response [and explanatory variables]. After developing such a model the fitted model can be used to make a prediction of the response. We just collect additional values of the explanatory variables and predict the response values.
Linear regression model often uses the least squares approach or MSE optimization. We’ll use the data set having 3 parameters (explanatory variables, covariates, input variables, predictor variables) and one observed value.
You can read in wiki on the Linear regression model and find a good post on how to apply Linear regression in the Data Analysis.
Theory 1
Mean squared error (MSE) and its optimization
Let’s first consider how to optimize the Linear regression by minimizing MSE.
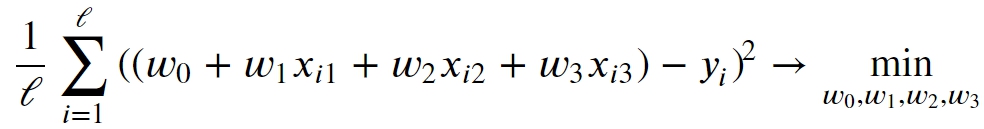
where
xi1, xi2, xi3 – input values of i-th input object of data set
yi – an observed value of i-th object
𝓁 – the amount of objects in a data set, the data set size.
Gradient descent of the Linear regression model
Since we have only 3 input values, the Linear regression model will be the following:
The Linear regression’s vector has 4 parameters (weights) therefore:
{ w0, w1, w2, w3 }
Based on them we can minimize the MSE thus finding optimal parameters of the Linear regression model.
The gradient step for the weights would be like the following:
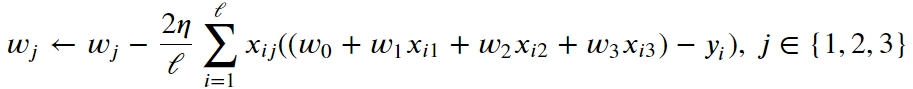
η – the step of gradient descent. It takes some art to find optimal η or make it dynamic based on iteration number.
The normal equation for the analytical solution
Finding the vector of optimal weights 𝑤 can also be done analytically. An algorithm wants to find a vector of weights 𝑤 such that the vector 𝑦 approximating the target feature is obtained by multiplying the matrix 𝑋 (consisting of all the features of the objects of the training sample, except the target) by the vector of weights 𝑤 .
That is, so that the matrix equation is satisfied: 𝑋*𝑤 = 𝑦
After some transformation (multiply on 𝑋T) we get:
𝑋T𝑋 * 𝑤 = 𝑋T𝑦
Because the matrix 𝑋T𝑋 is square, we may get the following for the vector of weights:
𝑤 = (𝑋 T𝑋)-1𝑋T𝑦
Matrix (𝑋T𝑋)-1𝑋T is the pseudo-inverse of a matrix 𝑋. In NumPy, such a matrix can be calculated using the numpy.linalg.pinv function. Yet, since calculation of pseudo-inverse matrix is difficult and unstable, we can also solve that using matrix normal equation:
𝑋 T𝑋 * 𝑤 = 𝑋 T𝑦
Thus we are to solve A*x = B matrix equation using numpy.linalg.solve method.
Business case and input data
We are given data with the adverting info, see the first 5 rows of it:
| TV | Radio | Newspaper | Sales | |
|---|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 | 22.1 |
| 2 | 44.5 | 39.3 | 45.1 | 10.4 |
| 3 | 17.2 | 45.9 | 69.3 | 9.3 |
| 4 | 151.5 | 41.3 | 58.5 | 18.5 |
| 5 | 180.8 | 10.8 | 58.4 | 12.9 |
The data display sales for a particular product as a function of advertising budgets (certain units) for TV, radio, and Newspaper media. We want predict future Sales (the last column, the response value) on the basis of this data [for future marketing strategies]. For that we build a linear regression model with the following parameters:
w0 + w1*TV + w2*Radio + w3*Newspaper
Now, optimizing the vector of weights we get the model that is optimal to predict Sales. Here are a few questions that we might answer using the linear regression model and its MSE:
- How does each budget parameter (TV, radio, and Newspaper) influence or contribute to Sales?
The linear regression model will answer that. - How accurately do we predict future sales?
The MSE will answer that.
Calculations for the Gradient decent
- Read the data into Data Frame
import pandas as pd
import numpy as np
adver_data = pd.read_csv('advertising.csv')We create NumPy X array from the TV, Radio, and Newspaper columns, and vector (matrix) y from the Sales column. And we output their shapes.
X = adver_data[['TV', 'Radio', 'Newspaper']].values
print('\nX shape:', X.shape)
y = adver_data[['Sales']].values
print('\ny shape:', y.shape)X shape: (200, 3)
y shape: (200, 1)
2. Normalize matrix X by substracting mean and dividing by std (Standard deviation, σ) of each column.
mean, std = np.mean(X,axis=0),np.std(X,axis=0)
print('mean values:', mean,'\nstd values:', std, '\n')
for el in X:
el[0] = (el[0] - mean[0])/std[0]
el[1] = (el[1] - mean[1])/std[1]
el[2] = (el[2] - mean[2])/std[2]
print('Normalized matrix X, head:\n', X[:5])mean values: [147.0425 23.264 30.554 ] std values: [85.63933176 14.80964564 21.72410606 ]
Normalized matrix X, head:
[[ 0.96985227 0.98152247 1.77894547]
[-1.19737623 1.08280781 0.66957876]
[-1.51615499 1.52846331 1.78354865]
[ 0.05204968 1.21785493 1.28640506]
[ 0.3941822 -0.84161366 1.28180188]]
3. Populate the matrix X with additional column of ones `1` so that we can process the coefficient 𝑤0 of the linear regression.
ones = np.ones((X.shape[0],1))
print('shape of ones:', ones.shape)
X = np.hstack((X, ones))
X[:5]shape of ones: (200, 1) array([[230.1, 37.8, 69.2, 1. ],
[ 44.5, 39.3, 45.1, 1. ],
[ 17.2, 45.9, 69.3, 1. ],
[151.5, 41.3, 58.5, 1. ],
[180.8, 10.8, 58.4, 1. ]])
4. Realize MSE based on y (observed values) and y_pred (predicted values). Note that both y and y_pred are of the same shape: (200, 1), that is [200 x 1] dimension matrix.
def mserror(y, y_pred):
return (sum((y - y_pred)**2)/y.shape[0] )5. Calculate the MSE for the y_pred equal to the median values of y.
med = np.array([np.median(y)] * X.shape[0])
med = med.reshape(y.shape[0],1)
print('\nmedian of y: ', med[0], '\nmed array shape:', med.shape)
print(med[:5])
MSE_med = mserror(y, med)
print('MSE value if median values as predicted: ', round(MSE_med, 3))
with open('1.txt', 'w') as f:
f.write(str(round(answer1 ,3)))median of y: [12.9]med array shape: (200, 1)[[12.9] [12.9] [12.9] [12.9] [12.9]] MSE value if median values as predicted: 28.346
6. Make a function of Normal equation:
𝑤 = (𝑋T𝑋)-1𝑋T𝑦
and calculate weights of the Linear regression model. For that we do the following:
- Calculate an inverse of a matrix, A-1. In Numpy, it is np.linalg.inv().
- Perform the matrix multiplication:
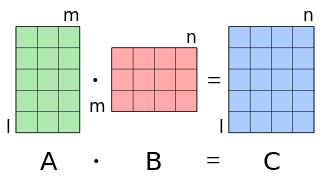
In Numpy the Matrix multiplication is defined as Matrix product of two arrays. Both expressions for the matrix multiplication are equal:
a @ bnp.linalg.matmul(a, b)
def normal_equation(X, y):
# np.linalg.inv(X.T @ X) @ X.T @ y
a = np.linalg.inv(X.T @ X)
b = a @ X.T
return b @ y
norm_eq_weights = normal_equation(X, y)
print('\nWeights calculated thru inv():', norm_eq_weights)
Weights calculated thru inv(): [[ 4.57646455e-02] [ 1.88530017e-01] [-1.03749304e-03] [ 2.93888937e+00]]
Just to note that the following Numpy operations are identical*. See the following code.
*np.dot(X, w) is identical only for 2-D matrixes.
print('X[1] @ w = ', X[1] @ w)
# np.dot(X, w) identical to matmul(X, w) only for 2-D matrixes
print('\n np.dot(X[1], w)= ', np.dot(X[1],w))
print('\n w[0]·X[1,0] + w[1]·X[1,1]+w[2]·X[1,2]+w[3]·X[1,3] =',\
w[0]*X[1, 0]+w[1]*X[1, 1]+w[2]*X[1, 2]+w[3]*X[1, 3])X[1] @ w = [11.80810892]
np.dot(X[1], w)= [11.80810892]
w[0]·X[1,0]+w[1]·X[1,1]+w[2]·X[1,2]+w[3]·X[1,3]= [11.80810892]
7. Another way to calculate the vector of Linear regression weights by solving
𝑤 = (𝑋T𝑋)-1𝑋T𝑦
where we compute the (Moore-Penrose) pseudo-inverse of a matrix X:
(𝑋T𝑋)-1𝑋T
# another way to calculate Linear regression weights
norm_eq_weights2 = np.linalg.pinv(X) @ y
print('\nWeights calculated thru pinv():', norm_eq_weights2)Weights calculated thru pinv():
[[ 4.57646455e-02]
[ 1.88530017e-01]
[-1.03749304e-03]
[ 2.93888937e+00]]
8. Calculate the Sales (predictions) if we do the mean spending for each of the parameters: TV, Radio, Newspapers. Mean for the normalized matrix X means zeros. The last (4-th) parameter in matrix 𝑋 is to work with w0; it is of the index 3 in the norm_eq_weights vector: norm_eq_weights[3, 0]. So we use 1 as the last item of input variables to match w0.
sales = np.array([0,0,0,1]) @ norm_eq_weights
print(round( sales.item(), 3))14.023
9. Compose the linear_prediction() function that calculates Sales prediction (y_pred) based on X and weights w.
N=10
def linear_prediction(X, w):
return np.dot(X, w) # the same as "X @ w" for 2D case
y_pred = linear_prediction(X, norm_eq_weights)
# we join the response values and predicted values
# in order to compare in one table.
yy = np.hstack((y, y_pred))
df = pd.DataFrame(yy[:N])
df.columns = ['Sales', 'Linear prediction of Sales']
print( df.head(N) )Sales Linear prediction (observed) of Sales 0 22.1 20.523974 1 10.4 12.337855 2 9.3 12.307671 3 18.5 17.597830 4 12.9 13.188672 5 7.2 12.478348 6 11.8 11.729760 7 13.2 12.122953 8 4.8 3.727341 9 10.6 12.550849
10. Calculate the MSE of y_pred of the Linear model found by the normal equation in point 6.
MSE_norm = mserror(y , y_pred)
print('MSE:', round(MSE_norm, 3))MSE: 2.784
Theory 2
Stochastic gradient descent (SGD)
Stochastic gradient descent differs from the gradient descent in that at each optimization step we change only one of weights (w0 or w1 or w2 or w3) thus decreasing the number of calculations. The needed optimization might be achieved faster than the gradient descent because less time [and recourses] is required for calculations.
In the SGD the corrections for the weights are calculated only taking into account one randomly taken object of the training sample/set. See the following:
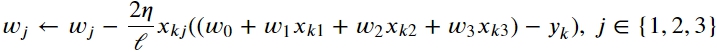
k – random index, k ∈ {1, … 𝓁}
Calculate SGD
1. We compose stochastic_gradient_step() function that implements the stochastic gradient descent step for the SGD of the Linear regression. The function inputs are the following:
- matrix X
- vectors y
- vector w
- train_ind – the index of the training sample object (rows of the matrix X), by which a change in the vector of weights is calculated
- 𝜂 (eta) – the step of gradient descent (by default, eta=0.01).
The function result will be the vector of updated weights. We’ll then call the function for each step of SGD. The function might be easily rewritten for a data sample with more than 3 attributes or input parameters.
def stochastic_gradient_step(X, y, w, train_ind, eta=0.01):
grad0 = X[train_ind][0] * ( X[train_ind] @ w - y[train_ind])
grad1 = X[train_ind][1] * ( X[train_ind] @ w - y[train_ind])
grad2 = X[train_ind][2] * ( X[train_ind] @ w - y[train_ind])
grad3 = X[train_ind][3] * ( X[train_ind] @ w - y[train_ind])
return w - 2 * eta / X.shape[0] * np.array([grad0, grad1, grad2, grad3])2. Perform the SGD for the Linear regression with the above function. The function stochastic_gradient_descent() takes the following arguments:
- X is the training sample matrix
- y is the vector of response values (the target attribute)
- w_init is a vector of initial weights of the model
- eta is a gradient descent step, (default value is 0.001)
- max_iter is the maximum number of iterations of gradient descent, (default value is 105)
- max_weight_dist is the maximum Euclidean distance between the vectors of the weights on neighboring iterations [of gradient descent] in which the algorithm stops (default value is 10-8)
- seed is a number used for the reproducibility of the generated pseudo-random numbers (default value is 42)
- verbose is a flag for printing information (for example, for debugging, False by default)
def stochastic_gradient_descent(X, y, w_init, eta=1e-3, max_iter=1e5, min_weight_dist=1e-8, seed=42, verbose=False):
# Initialize the distance between the weight vectors
# A large number as initial weight distance
weight_dist = np.inf
# Initialize the vector of weights
w = w_init
# Error array for each iteration
errors = []
# Iteration counter
iter_num = 0
# Generate `random_ind` using a sequence of [pseudo]random numbers
# we use seed for that
np.random.seed(seed)
# Main loop
while weight_dist > min_weight_dist and iter_num < max_iter:
random_ind = np.random.randint(X.shape[0])
prev_w = w
w = stochastic_gradient_step(X, y, w, random_ind, eta)
weight_dist = np.linalg.norm(w - prev_w)
errors.append(mserror(y, X @ w))
iter_num +=1
return w, errors3. Execute SGD. Now we run 105 iterations of stochastic gradient descent. The initial weight vector w_init consists of zeros, namely np.zeros((4, 1)) in Numpy.
%%time
stoch_grad_desc_weights, stoch_errors_by_iter = stochastic_gradient_descent(X, y, np.zeros((4, 1)))
print('Iteration count:', len(stoch_errors_by_iter))Result is the following:
Wall time: 1.63 sIteration count: 100000
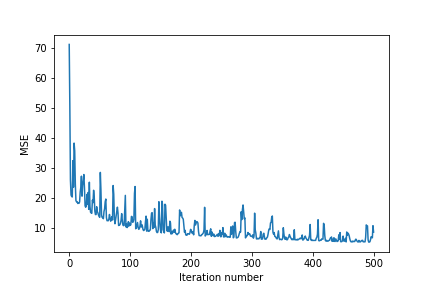
4. Let’s plot MSE of SGD on the first 500 iterations. One can see that the MSE does not necessarily decrease at each iteration.
%pylab inline
plot(range(500), stoch_errors_by_iter[:500])
xlabel('Iteration number')
ylabel('MSE')
# save image if needed
plt.savefig(
'linear-regression-SGD-50.png',
format='png',
dpi=72
)
5. Let’s show the Linear regression model weights vector and MSE at the last SGD iteration.
print('Linear regression model weights vector:\n', stoch_grad_desc_weights, '\n')
print('MSE at the last iteration:', round(stoch_errors_by_iter[-1], 3))Linear regression model weights vector:
[[0.05126086]
[0.22575809]
[0.01354651]
[0.04376025]]
MSE at the last iteration: 4.18
6. Now we may predict Sales, the vector y_pred, for any input variables (X) using the Linear model: y_pred = X @ w. Remember that X is a normalized matrix in the model. That means that as we set it up we need to scale by substracting mean value and dividing on std, σ.
X = (X – mean)/std
y_pred = X @ w
mean = [147.0425 23.264 30.554 ] std = [85.63933176 14.80964564 21.72410606 ]
Besides, we may count MSE for each predicted Sale (y_pred) value.
MSE = mserror(y , y_pred)
or
MSE = sum((y - y_pred)**2)/len(y)
Conclusion
The Linear regression model is a good fit for Data Analysis for data with observed values. The Stochastic gradient decent SGD is more preferred than just the Gradient decent since the former requires fewer calculations while keeping a needed convergence of Linear regression model.
