import warnings
warnings.filterwarnings("ignore")

from matplotlib.colors import ListedColormap
from sklearn import model_selection, datasets, linear_model, metrics
import numpy as np

%pylab inline

1. Data generation

We choose a dataset of 2 features, labels forming 2 clouds.

• centers – number of classes
• cluster_std – standart deviation

blobs = datasets.make_blobs(centers = 2, cluster_std = 5.5, random_state=1)

Let’s visualize datasets in colors.

colors = ListedColormap(["red", "blue"])
pylab.figure(figsize(10, 10))
pylab.scatter([x[0] for x in blobs[0]], [x[1] for x in blobs[0]], c=blobs[1], cmap=colors)

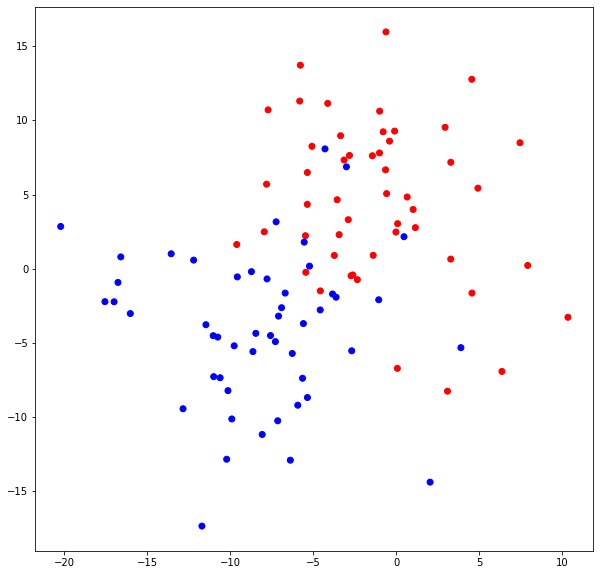
Now we split the blobs dataset into the train and test sets.

train_data, test_data, train_labels, test_labels \
   = model_selection.train_test_split(blobs[0], blobs[1], \
   test_size = 0.3, random_state = 1)

2. Linear classification models

2.1 RidgeClassifier

We’ll create/build the linear classifier named RidgeClassifier.

ridge_classifier = linear_model.RidgeClassifier(random_state = 1)

We train the classifier object: pass to it the train data and the train labels generated earlier.

ridge_classifier.fit(train_data, train_labels)

Now we check how well the classsifier has been trained.

We apply the test data to get predictions.

ridge_predictions = ridge_classifier.predict(test_data)

Now we output the test labels (response values) and the predicted labels, ones generated by the classifier.

print("Actual labels:\n", test_labels)
print("\nPredicted labels:\n", ridge_predictions)

Actual labels:
 [0 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 0 0 0 1 1 1 1 0 0 1]
Predicted labels:
 [0 0 0 1 0 1 0 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 1 1 1 1 0 0 1]

We now rate the classification model quality.

round(metrics.accuracy_score(test_labels, ridge_predictions), 2)

We output the features weights and intercept for the following approximation function:

print("[w1, w2]:", ridge_classifier.coef_ )

print("[w0]:",ridge_classifier.intercept_ )

2.2 Logistic Regression

The Logistic Regression is another model that we’ll train with the labeled data.

Create a classifier with the default parameters. Some of them are shown below:

• penalty = L2. Taken as a parameter of regularization.
• tolerance = 0.0001

log_regressor = linear_model.LogisticRegression(random_state = 1)

We train the set with the method fit().

log_regressor.fit(train_data, train_labels)

LogisticRegression(random_state=1)

We get predictions of the trained model. Besides prediction labels, the logistic regression build the probability model. That means that it may return a probability with which each object belongs to a certain class. Method predict_proba() returns the probability array.

lr_predictions = log_regressor.predict(test_data)
lr_proba_predictions = log_regressor.predict_proba(test_data)

print("Actual labels:\n", test_labels)
print("\nPredicted labels:\n", lr_predictions)

Actual labels:
 [0 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 0 0 0 1 1 1 1 0 0 1]
Predicted labels:
 [0 1 1 1 0 1 0 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 1 1 1 1 0 0 1]

We output the probability predictions. For each object we get 2 probability values. These define probability if it pertains to label “0” or “1”.

print(lr_proba_predictions[:10])

[[9.99254667e-01 7.45333217e-04]
 [4.08279523e-01 5.91720477e-01]
 [4.90541791e-01 5.09458209e-01]
 [3.78296027e-03 9.96217040e-01]
 [7.32221196e-01 2.67778804e-01]
 [2.44262899e-01 7.55737101e-01]
 [9.93761113e-01 6.23888724e-03]
 [9.78405579e-01 2.15944205e-02]
 [9.55344987e-01 4.46550128e-02]
 [1.68318566e-01 8.31681434e-01]]

We now rate the Logistic regression and RidgeClassifier models; compare quality.

print("Logistic regression", round(metrics.accuracy_score(test_labels, lr_predictions), 3))
print("\nRidgeClassifier:", round(metrics.accuracy_score(test_labels, ridge_predictions), 3))

Logistic regression 0.8
RidgeClassifier: 0.867

3. Quality assessment of cross-validation

3.1 Evaluate a score by cross-validation

The library provides a useful function cross_val_score() to evaluate a score of method by cross-validation.

• [trained] method: ridge_classifier
• data: blobs[0]
• labels: blobs[1]
• metric, scoring parameter. ‘accuracy’ – 1/N*∑[a(xi)==yi]
• cv denotes a cross-validation splitting strategy. cv is the K parameter in the KFold strategy.

ridge_scoring = model_selection.cross_val_score(ridge_classifier, blobs[0], blobs[1], scoring = "accuracy", cv = 10)

lr_scoring = model_selection.cross_val_score(log_regressor, blobs[0], blobs[1], scoring = "accuracy", cv = 10)

print("RidgeClassifier:\n", ridge_scoring)
print("\nLogistic regression scoring:\n", lr_scoring)

RidgeClassifier:
 [0.8 0.9 0.9 0.9 1.  1.  0.7 0.9 0.9 0.8]
Logistic regression scoring:
 [0.8 0.9 0.9 0.9 1.  1.  0.7 0.9 0.9 0.8]

Let’s view the scoring statistics:

print("Ridge mean:{}, max:{}, min:{}, std:{}"\
    .format(round(ridge_scoring.mean(), 3), ridge_scoring.max(), \
    ridge_scoring.min(), round( ridge_scoring.std(), 3)))

print("Log mean:{}, max:{}, min:{}, std:{}"\
    .format(round(lr_scoring.mean(), 3), lr_scoring.max(), \
    lr_scoring.min(),  round( lr_scoring.std(), 3)))

3.2 Evaluate a score by cross-validation with specified scorer and cv_strategy

Suppose we want to score a non-standart metric and we want to specify the cross-validation strategy.

We first define a scorer and specify cross-validation stratagy:

scorer = metrics.make_scorer(metrics.accuracy_score)
cv_strategy = model_selection.StratifiedShuffleSplit(n_splits=20, test_size = 0.3, random_state = 2)
cv_strategy.get_n_splits(blobs[1])

ridge_scoring = model_selection.cross_val_score(ridge_classifier, \
 blobs[0], blobs[1], scoring = scorer, cv = cv_strategy)

lr_scoring = model_selection.cross_val_score(log_regressor, \
 blobs[0], blobs[1], scoring = scorer, cv = cv_strategy)

print("Ridge mean:{}, max:{}, min:{}, std:{}"\
   .format(round(ridge_scoring.mean(), 3), ridge_scoring.max(), \
    ridge_scoring.min(), round( ridge_scoring.std(), 3)))

print("Log mean:{}, max:{}, min:{}, std:{}"\
    .format(round(lr_scoring.mean(), 3), lr_scoring.max(), \
    lr_scoring.min(),  round( lr_scoring.std(), 3)))